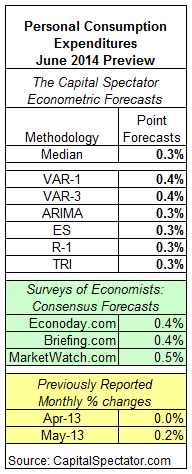
Tomorrow’s update on US personal consumption spending for June is expected to report a gain of 0.3% vs. the previous month, based on The Capital Spectator’s median econometric point forecast. That’s slightly higher than the reported 0.2% rise for May.

Meanwhile, the Capital Spectator’s median forecast for June is slightly below a trio of consensus estimates based on recent surveys of economists.

Keep in mind that the interval forecasts at the 95% confidence level reflect a relatively wide spectrum of outcomes around the point forecasts. Here’s a closer look at the numbers, followed by brief summaries of the methodologies behind The Capital Spectator’s projections:

VAR-1: A vector autoregression model that analyzes the history of personal income in context with personal consumption expenditures. The forecasts are run in R with the “vars” package.

VAR-3: A vector autoregression model that analyzes three economic time series in context with personal consumption expenditures. The three additional series: US private payrolls, personal income, and industrial production. The forecasts are run in R with the “vars” package.

ARIMA: An autoregressive integrated moving average model that analyzes the historical record of personal consumption expenditures in R via the “forecast” package to project future values.

ES: An exponential smoothing model that analyzes the historical record of personal consumption expenditures in R via the “forecast” package to project future values.

R-1: A linear regression model that analyzes the historical record of personal consumption expenditures in context with retail sales. The historical relationship between the variables is applied to the more recently updated retail sales data to project personal consumption expenditures. The computations are run in R.

TRI: A model that’s based on combining point forecasts, along with the upper and lower prediction intervals (at the 95% confidence level), via a technique known as triangular distributions. The basic procedure: 1) run a Monte Carlo simulation on the combined forecasts and generate 1 million data points on each forecast series to estimate a triangular distribution; 2) take random samples from each of the simulated data sets and use the expected value with the highest frequency as the prediction. The forecast combinations are drawn from the projections generated by the models above, as computed in in R with the “triangle” package.