Probing the link between financial markets and chaotic states, fractals, and related topics dates to the 1960s, when mathematician Benoit Mandelbrot effectively launched this line of research with his seminal study of cotton prices that documented “recurring patterns at every scale in data,” notes Wikipedia. The subject of chaos and how to exploit it for profit is an ongoing arena for study, albeit with mixed results. The Hurst exponent, for instance, attracted a lot of interest a number of years ago, in part due to an influential and widely read review of the indicator by Edgar Peters in his 1991 book Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility.

There’s still plenty debate about how one might apply the Hurst exponent and related metrics in the day-to-day business of money management. Yet the field of chaos theory remains an intriguing and potentially rewarding area for research. My own interest in this corner has waxed and waned over the years, but I was intrigued anew when I read David Varadi’s brief but thought-provoking essay in March on “Using a Self-Similarity Metric with Intraday Data to Define Market Regimes.” As he explains,

Self-dissimilar objects are associated with complexity and chaos. Several mathematicians (including Mandelbrot) have observed that markets are clearly non-gaussian or non-normal. Markets exhibit “fat-tails” and have a distribution that shares more in common with a Levy distribution than the normal distribution which is used frequently in quantitative finance. But the market does not have a constant distribution- at times the market behavior is fairly normal in character while at other times the market is wild and unpredictable. The question is how we can effectively determine which regime the market is in so that we can apply the appropriate trading strategies to mitigate risk.

Varadi offers a simple but potentially useful answer with a measure of self-similarity based on analyzing the market’s intraday range and how it changes in the short term relative to a longer-run window. As a basis for further exploration, let’s take a stab at translating Varadi’s instructions by generating the data in R (see code below) for analyzing the US stock market via the S&P 500.

Varadi advises that “values above 0.5 indicate that the market is in a ‘chaos’ regime and is much less predictable and non-stationary; values below 0.5 indicate that the market is stable and much more predictable.”

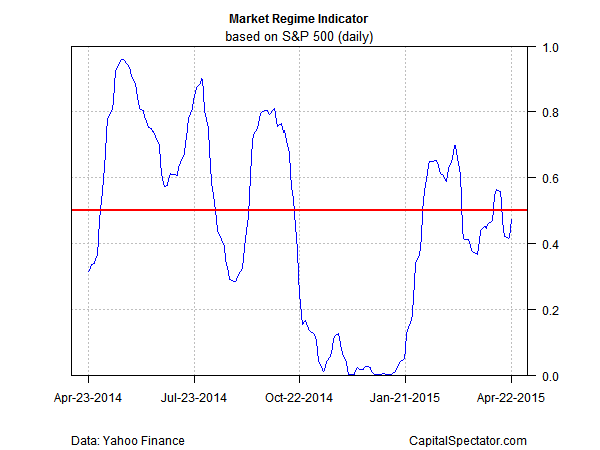
Here’s a look at the indicator over the past year:

Note that this metric has been bouncing around the 0.5 mark recently (red line in chart above), which suggests an equilibrium/neutral condition. That’s in contrast with the stable regime (below 0.5) that prevailed in late-2014 through this past January.

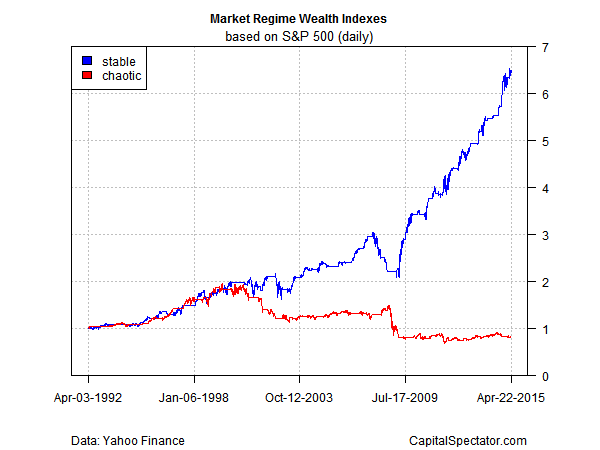
Why is any of this relevant? Because most of the gains in the stock market through time are generated during the stable regime. As an illustration, let’s reproduce a chart in Varadi’s post, where he separates the stable regime from its chaotic counterpart and generates wealth indexes for each data set. The key message, he notes, is that “the market performs quite poorly in ‘chaos’ conditions, and seems to make all of its long-term returns in the ‘stable’ regime.”

The notion that trending/momentum factors are valuable sources of risk premia is old news, of course. The challenge is figuring out when market conditions are ripe for earning a profit from these factors… and when they’re not.

Varadi’s indicator is hardly the last word on modeling the market’s evolution between chaos and stability, but it’s a useful first approximation. As such, it’s a good benchmark for additional research and looking for possibilities for enhancing this signal. (For additional perspective on this indicator, take a look at his follow-up piece here.)

R Code to generate the data in the charts above:

[code language=”r”]

library(TTR)
library(zoo)
library(quantmod)

# download daily S&P 500 data
sp500 <-getSymbols(‘^gspc’,from=’1990-12-31′,auto.assign=FALSE)

# Varadi outlines 6 steps for calculating his market-regime indicator:

# 1. "Find the high minus the low for each day going back 10 days."
# 2. "Take the sum of these values (sum of the pieces)."
hi.lo <-Hi(sp500)-Lo(sp500)
hi.lo.10 <-rollapply(hi.lo,10,sum)

# 3. "Find the 10-day range by taking the 10-day maximum (including the highs)
# and subtracting out the 10-day minimum (whole range)."
hi <-Hi(sp500)
lo <-Lo(sp500)
hi.10 <-rollapply(hi,10,max)
lo.10 <-rollapply(hi,10,min)
hi.lo.diff <-hi.10-lo.10

# 4. "Divide the sum of the pieces by the whole range–
# this is a basic measure of fractal dimension/complexity."
frac.dim.complex <-hi.lo.10/hi.lo.diff

# 5. "Take the 60-day average of the 10-day series of the complexity values–
# this is the "chaos/stability" metric."
frac.dim.complex.60 <-na.omit(SMA(frac.dim.complex,60))

# 6. "Use either the 252-day normsdist of the z-score
# or the percentile ranking of the chaos/stability metric."
#regime <-na.omit(pnorm(scale(frac.dim.complex.60)))
regime <-na.omit(runPercentRank(frac.dim.complex.60,252))

# values above .5 indicate that the market is in a "chaos" regime
# and is much less predictable and non-stationary,
# values below .5 indicate that the market is stable
# and much more predictable.

# Separate chaotic data from stable data
# and generate wealth indexes

# calculate S&P 500 daily % return
sp500.ret <-na.omit(ROC(Cl(sp500),1,"discrete"))

# create wealth index for stable regime periods
regime.stable.signal <-ifelse(regime < 0.5,1,0)
regime.stable.ret <-regime.stable.signal*tail(sp500.ret,length(regime.stable.signal))
regime.stable.index <-cumprod(1+regime.stable.ret)

# create wealth index for chaotic regime periods
regime.chaos.signal <-ifelse(regime > 0.5,1,0)
regime.chaos.ret <-regime.chaos.signal*tail(sp500.ret,length(regime.chaos.signal))
regime.chaos.index <-cumprod(1+regime.chaos.ret)

# combine wealth indexes for charting
regimes.2 <-cbind(regime.stable.index,regime.chaos.index)

### END

[/code]