The world is awash with backtests that lay claim to new portfolio techniques that provide superior results for managing risk, juicing return, or both. What’s often missing is a robust stress test to confirm that the good news is more than a statistical anomaly. Crunching the numbers on a single run of history that looks encouraging is one thing; taking the backtest to the next level by simulating results across a range of alternative scenarios as a proxy for kicking the tires on the future is something else entirely. Not surprisingly, only a tiny sliver of the strategies that look good on paper can survive this higher standard. That’s a problem if you’re intent on publishing a regular stream of upbeat research reports that appear to open the door to money-management glory. But for investors wary of committing real money to new and largely untested portfolio strategies, stress testing is critical for separating the wheat from the chaff.
As a simple example, let’s review the results for a widely respected tactical asset allocation strategy that was originally outlined by Meb Faber in “A Quantitative Approach to Tactical Asset Allocation.” The original 2007 paper studied a simple system of using moving averages across asset classes to manage risk. The impressive results are generated by a model that compares the current end-of-month price to a 10-month average. If the end-of-month price is above the 10-month average, buy or continue to hold the asset. Otherwise, sell or hold cash for the asset’s share of the portfolio. The result? A remarkably strong return for what we’ll refer to as the Faber strategy over decades, in both absolute and risk-adjusted terms, vs. buying and holding the same mix of assets.
For illustrative purposes, let’s re-run the data with just two ETFs—a simple 60%/40% US stock/bond mix based on a pair of ETFs: SPDR S&P 500 ETF (SPY) and iShares 7-10 Year Treasury Bond (IEF) for a sample period that runs from the end of 2003 through the present. As the chart below shows, the Faber strategy looks quite impressive vs. a buy-and-hold portfolio that sets the initial weights to 60%/40% and leaves the rest to Mr. Market.
So far, so good. The Faber strategy performs in line with the results in the original study. Applying tactical asset allocation by way of the paper generated less volatile results with a moderately higher return over the sample period. The annualized Sharpe ratio (a risk metric that adjusts return based on volatility) for this version of the Faber strategy over the 2003-2016 period is 0.87. That’s a solid premium over the buy-and-hold’s Sharpe ratio of 0.60. Taken at face value, the higher Sharpe ratio tells us that the Faber strategy is superior even after adjusting for risk (return volatility).
But let’s take this up a notch and run a Monte Carlo analysis on the Faber strategy. The plan is to re-run the strategy multiple times and collect the results. In other words, we’re going to simulate alternative histories for a deeper read on what the future might bring. Rather than rely on one backtest, albeit one based on actual history, this technique allows us to consider how the Faber strategy might perform if history could be repeated thousands of times with different results.
The heavy lifting for running the Monte Carlo test will be performed in R. The key piece of code is the sample() command. By resampling the Faber strategy’s actual returns we can produce alternative outcomes—10,000 outcomes in the case of this test.
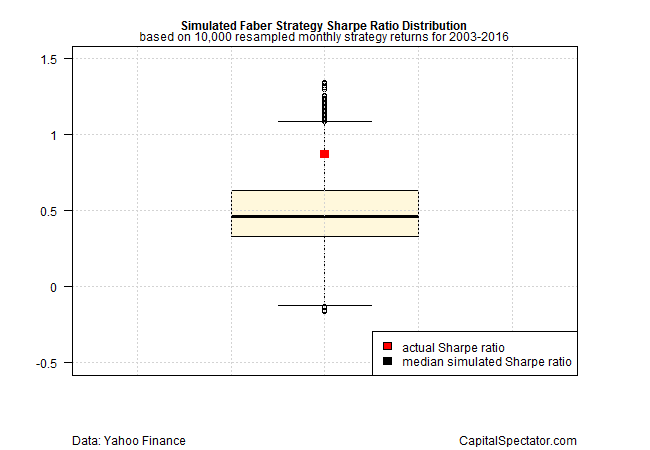
The boxplot below summarizes the output in terms of the range of annualized Sharpe ratios for the 10,000 simulated runs. Note the red box, which marks the 0.87 Sharpe ratio in the original backtest using actual data. But this result looks quite high in the context of the simulated data. The implication: the original backtest outlined above may have oversold the strategy’s results in terms of what we can expect going forward with the out-of-sample performance.
Indeed, the original 0.87 Sharpe ratio is well above the median Sharpe ratio of 0.46 for the simulated data and the 0.63 SR at the upper level of the interquartile range (the 75th percentile). The results don’t necessarily invalidate the Faber strategy, but the elevated Sharpe ratio in the original test suggests that the sample period (2003-2016) may have been an unusually fertile period that isn’t likely to deliver a repeat performance any time soon if ever.
In short, it appears that we should manage expectations down relative to the original backtest. In turn, the stress test could be the basis for revising the strategy or turning to another methodology for managing money.
To be fair, a robust stress test would run a series of analytics beyond Sharpe ratio simulations. But this toy example is still a powerful reminder that first impressions with backtests can be misleading and, in the worst cases, hazardous to your wealth.
The challenge is developing reasonable expectations and all too often backtesting procedures fall short. Keep in mind too that there’s a reason you’ll really find a backtest that highlights poor results: research that reveals failure tends to be buried.
The good news is that there’s a spectrum a techniques (see here, here and here, for instance) for deciding if the initial results of an encouraging backtest have a reasonable chance to hold up in the real world going forward. To be fair, the Faber strategy overall has been tested extensively by analysts and continues to offer upbeat results, albeit with all the standard caveats. But that’s the exception to the rule.
It’s a safe assumption that most backtests in the grand scheme of research efforts that see the light of day will fail to deliver anything close to the stellar results outlined. Fortunately, a multi-faceted stress test can go a long way in reducing the risk that the research du jour is leading you astray.

Pingback: Time to Stress Test Your Portfolio - TradingGods.net
hey james
tx for the post.
“By resampling the Faber strategy’s actual returns we can produce alternative outcomes—10,000 outcomes in the case of this test.” – can u confirm you are:
1) simulating the 60/40 port 10000x
2) running faber strategy on each of the 10000 runs of alternative returns for the 60/40 port
3) tabulate distribution of faber strategy for each of the 10000 alt histories and display via box/whisker plot
tx!
davecan99,
Yes, that’s the process in the code. I’ve written a function that resamples the original return data for each of the two ETFs and then recalculates, 10,000 times, the Faber strategy based on new resamples. The function than spits out the Sharpe ratio at the end of each run. I’m using the replicate() command in R to do the 10,000 runs, although lapply() works too.
–JP
Unless you’re sampling *blocks* of returns, with blocksize greater than Faber’s 10 months, then you’re destroying serial dependence within blocks of 10 months. For example, a straightfoward application of the sample() function to a daily return time series thoroughly destroys serial dependence within the time series.
If employing ‘sample()’ this way then it’s no surprise that a timing method like the SMA rule, when run on data with no serial dependence, doesn’t work i.e. doesn’t achieve the Sharpe ratio seen on the original data that does have serial dependence.
If you want to test Faber’s method you need to employ the ‘sample’ function in a way that samples *blocks* of returns, i.e. ‘block bootstrap’ , with blocksize greater than 10 months (about 200 trading days).
There is extensive literature on ‘block bootstrap’ for time series.
ted thedog,
Yes, good point. In fact, I use block resampling and have written about it:
http://www.capitalspectator.com/a-better-way-to-run-bootstrap-return-tests-block-resampling/
But there are only so many technical points one can cram into one short blog post. In any case, the point here isn’t about getting into the weeds about resampling techniques, important as that is. Rather, I’m simply trying to make the point that it’s essential to test a strategy on a number of levels before embracing an underlying study as gospel.
In any case, thanks for reminding everyone (myself included) about the value of block resampling.
–JP
Am very glad you had a post on block bootstrapping, very sorry I missed it, just read it now. As you discussed, it’s a very valuable technique.
But we’re coming to different conclusions about what boostrapping says about the Faber strategy:
You’re looking at the distribution of Sharpe, I looked at distribution of returns and also distribution of maxdrawdown.
Your graph shows how maxdd was reduced by use of the SMA strategy in the real i.e. non-bootstrapped data.
I’m curious if you noticed if the maxdrawdowns continued to be reduced in the block bootstrapped data?
I found maxdrawdowns continued to be reduced in the boostrapped samples (btw, I went back to 1993 using just equities, so also saw the tech crash).
Also that the distribution of strategy returns was just slightly shifted lower than buy&hold returns.
Therefore I came to a different conclusion than you, I concluded that boostrapping supported Faber’s SMA strategy:
the SMA strategy significantly reduces drawdowns at a slight expense to returns.
The meboot package is not a straightforward implementation of block boostrapping and I’m not sure I understand it.
I used a very straightforward implementation of block boostrapping, so I tend to believe it.
ted thedog,
Yes, I agree that the Faber strategy is generally productive and holds up quite well to out of sample. It’s certainly one of the stronger strategies in terms of additional testing. To be fair, my toy example used on 2 funds and so, well, it really wasn’t fair. As Faber has discussed, it’s best to use a wider array of funds/asset classes; I didn’t in this case, mostly for expediency. In other tests I’ve run, including a few that show up on the blog (see here: http://www.capitalspectator.com/tactical-asset-allocation-for-the-real-world/), the Faber strategy holds up quite nicely with a broader array of assets. In short, it’s really not worth discussing this 2-fund test since it’s merely a device to make a point about testing strategies.
That said, while I’m a fan of block bootstrapping, it comes with its own set of issues, including deciding how large the blocks should be, should they overlap?, etc. Fortunately, R has resources to help minimize such issues. The b.star command in the np package, for instance, is useful for selecting block size.
As for meboot’s complexity, there are alternatives to consider, including tsboot {boot] and tsbootstrap {tseries}.
–JP
hi
right so the point of the post is twofold
1) the use of monte carlo simulations to test a portfolio can be helpful in analyzing how good a strategy is (i come from pension/insurance world where simulations are used all the time – rarely are backtests employed, so this makes a lot of sense to me).
2) the nature of the simulations matters – eg if you are simulating assets assuming they have serial dependence, or not, matters, in terms of how a strategy might behave. that’s why we usually start with a simulator that reflects properties of asset classes we “believe’ to be stylized facts and then move on to testing investment strategies using these simulations. we’ll also build in toggles to turn on/off things like serial dependence, to see if a strategy is robust to this assumption or not.
thoughts?
Pingback: 09/12/16 – Monday’s Interest-ing Reads | Compound Interest-ing!
Dave,
I think you’re on the right track with your thinking. I’m inclined to run backtests and Monte Carlo simulations and compare the results. Are there big differences? Or do the results generally support one another? Ditto for simululating with serial dependence and without–for the underlying asset returns as well as for the portfolio performance. Sometimes you can learn a lot by toggling on and off, as you say. The caveat is that these tests tend to do quite well in finding reasons to cast doubts on a strategy rather than endorse it directly. But that’s still valuable information. If you can’t find serious defects with a strategy, then maybe it’s pretty good after all.
–JP