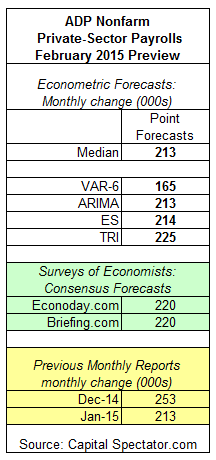
Private nonfarm payrolls in the US are projected to increase by 213,000 (seasonally adjusted) in tomorrow’s February update of the ADP Employment Report, based on The Capital Spectator’s median point forecast for several econometric estimates. The median projection matches January’s increase.

Two estimates based on recent surveys of economists point to a moderately bigger gain for the ADP Employment Report in February relative to The Capital Spectator’s median projection.

Here’s a closer look at the numbers, followed by brief summaries of the methodologies behind the forecasts that are used to calculate The Capital Spectator’s median prediction:

VAR-6: A vector autoregression model that analyzes six economic time series in context with the ADP private payroll employment. The six additional series: the ISM Manufacturing Index, industrial production, index of weekly hours worked, US stock market (Wilshire 5000), spot oil prices, and the Treasury yield spread (10 year Note less 3-month T-bill). The forecasts are run in R with the “vars” package.

ARIMA: An autoregressive integrated moving average model that analyzes the historical record of the ADP private payroll employment data in R via the “forecast” package.

ES: An exponential smoothing model that analyzes the historical record of the ADP private payroll employment data in R via the “forecast” package.

TRI: A model that’s based on combining point forecasts, along with the upper and lower prediction intervals (at the 95% confidence level), via a technique known as triangular distributions. The basic procedure: 1) run a Monte Carlo simulation on the combined forecasts and generate 1 million data points on each forecast series to estimate a triangular distribution; 2) take random samples from each of the simulated data sets and use the expected value with the highest frequency as the prediction. The forecast combinations are drawn from the following projections: Econoday.com’s consensus forecast data and the predictions generated by the models above. The forecasts are run in R with the “triangle” package.